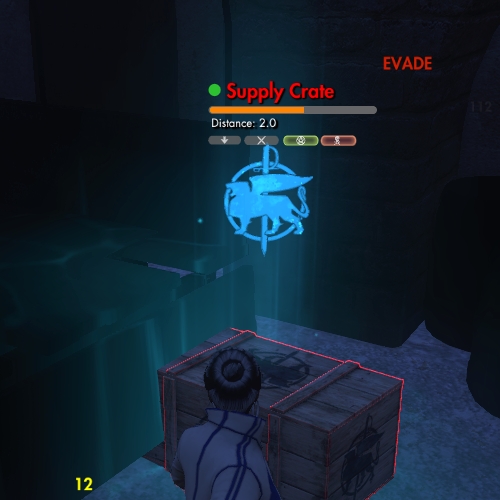
In TSW, you hit chests in scenarios to break them open and get out mines that you can use to mitigate the desperate unfairness of it all. That's not the reason I'm showing this picture, though: the reason I'm showing it is that word, EVADE.
I swung at a chest with a sword and somehow the chest evaded my blow.
It's a chest. Chests can't move. How did it evade my swing of the sword? It's not just swords, they can evade bullets and flamethrowers.
This is an example of something so common in today's MMOs that people barely register it as being weird. Evasion is a concept in TSW combat which means that the attacker failed to hit the defender — they missed, in other words. However, as the main statistic that determines whether the attacker hits or misses is associated with the defender, it can't be "the property of being missed", it has to be something that more like "the property of being able to avoid being hit"' in this context, "evade" works. Except, when you have something large and inanimate like a chest, there shouldn't be any chance of missing — it should be a guaranteed hit. Unless you adjust combat calculations by type of weapon and target, though, that simply can't happen. If combat has deep in in its DNA the concept of evasion, then chests. like everything else, can evade (because what actually happens is that the attacker sometimes misses — even if the defender has a zero evade rating).
We did used to have combat adjustments by weapon and target in the old text MUD days. It's not hard to implement. Even in non-computer games such as Dungeons & Dragons, where calculations are done manually and are therefore expensive, there are plenty of weapons which do more damage to one type of creature than another (maces against skeletons: good; arrows against skeletons: bad). Deciding which weapon to use from your collection was an interesting decision which made for interesting gameplay. If you know that undead are susceptible to warhammers and dryads are suceptible to axes and gelatinous cubes are susceptible to fireballs, you have to plan what tools to use dependent on what you expect to come up against. Flexibility is important. As I've mentioned before, if I have a spell called "exsanguinate" then it should work brilliantly against things that have blood to be sucked out of them, but not so great against robots, rocks or chests.
Interestingly, the rumours concerning the Tokyo expansion for TSW (expected in February — as in last month) seem to suggest that the accompanying improvements to the combat system will have something like this. There's a concept of an "aegis", where different types are effective against specific kinds of monster. That should introduce more strategy, but it does make me wonder why they didn't just have it for regular weapons and spells rather than adding it on as an extra layer (atop the augment layer they already added).
If I have a spell that shoots fire and I cast it at some kind of demon from hell that has flames writhing up its body, then either I should do no damage (because it's immune) or I should do extra damage (because my attack is in the same element as its being). What shouldn't happen is that I do the same damage as if I cast it at a zombie or a chest.
I really have no idea how today's MMOs got this way.